If an Automata makes more than one transition for a single input symbol from a given state, then the next state of the automata becomes unpredictable. Such a type of automata is said to be NFA. Suppose the finite automata are modified in such a way that from a state on an input symbol, zero or more transitions are permitted. In that case, the corresponding finite automata is called a Non Deterministic Finite Automata (NFA)
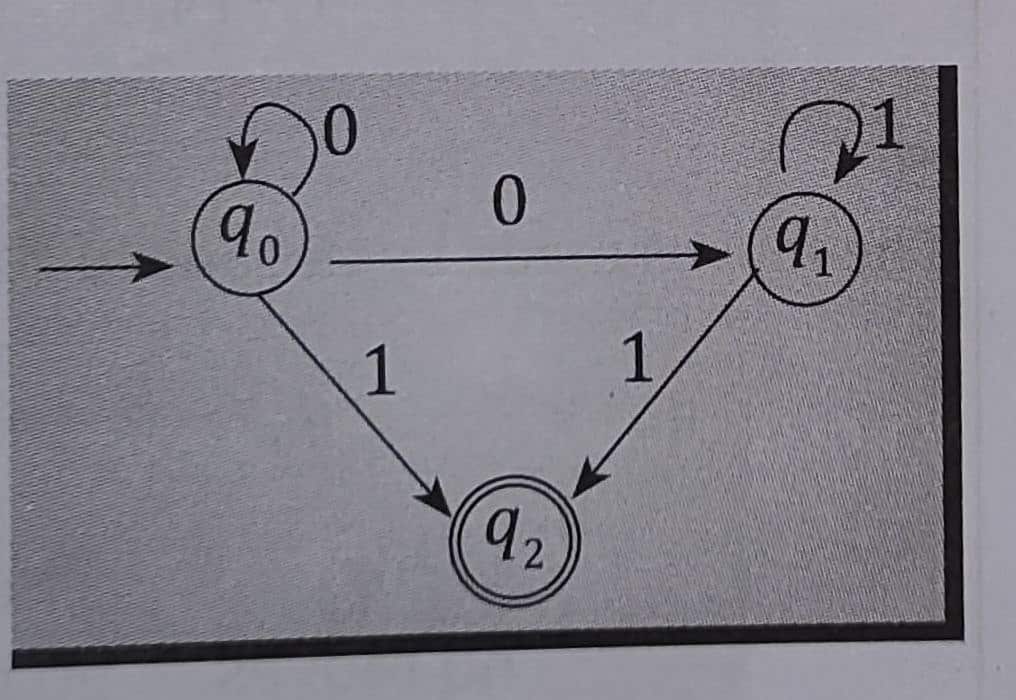
For example, consider the following finite automata
What will be the next state if the automation is in state q, and the input symbol is 0? From the figure, it is clear that the next state will be either q, or q₁. Thus some moves of the machine cannot be determined uniquely by the input symbol from the present state, such machines are called NFA.
Mathematical Representation of NFA
Definition: NFA is a five tuple, (Q, E, 8, 9, F)
Where
- Q is a non-empty finite set of states.
- Σ is a non-empty finite set of input symbols.
- q, Q, is the start state
- FCQ is the set of accepting/final states
- 8: QXE→ 2º, is the transition function.
2º is the power set of Q, which is the set of all subsets of Q.
Note: In an NFA there can be zero, one or more transitions on an input symbol.
See Also: What is Grammar in TOC?
e- NFA
In some situations, it would be useful to enhance NFAS by allowing transitions that are not triggered by any input symbol; such transitions are called E – transitions. If there is a transition from one state to another state without any input (E), it is called E – transition. An NFA with zero or more Є – transitions is called an Є – NFA.
Mathematical Representation of E – NFA
Definition: E – NFA is a five tuple (Q, E, 8, qo, F)
Where
- Q is a non-empty finite set of states.
- Σ is a non-empty finite set of input symbols.
- q, Q, is the start state
- FCQ is the set of accepting/final states
- 8: QX (UE)→ 2º, is the transition function.
Based on the current state there can be a transition to other states with or without any input symbols.

Comparison of DFA, NFA and e-NFA
| DFA | NFA | e-NFA |
|---|---|---|
| DFA is a 5-tuple D= (Q, Σ, 8, 9, F) 8:QXΣ→Q | NFA is a 5-tuple N = (Q, Σ, 8, 90, F) 8: QX-2º | e-NFA is a 5-tuple E = (Q, Σ, 8, 90, F) 8: QX(UE) → 2º |
| DFA can have only one transition from a state on an input symbol | NFA can have zero, one or more transitions from a state on an input symbol | e- NFA is an NFA with zero or more E-transitions |
| Difficult to construct | Easy to construct | Easy to construct |
| Less powerful since at any point in time it will be in only one state | More powerful than DFA since at any point in time it will be in more than one state | More powerful than NFA since at any point in time it will be in more than one state with or without giving any input. |
Define Symbol, Alphabet with an example
The symbol is an abstract entity.
Example:
Letters: a, b, c,_ _ _
Digits: 0, 1, 2_ _ _
Alphabet (Σ): An Alphabet or character set is a finite non-empty set of symbols.


